CAMELIA
CAMELIA (Current Advance Method Et cycLIc leApfrog) is a hybrid kinetic code where electrons are
considered as a massless, charge neutralizing fluid,
whereas ions are
described by a particle-in-cell model and are advanced
by the Boris scheme that requires
the fields to be known at half time steps ahead of the
particle velocities. This is achieved by advancing the current density to
this time step with only one computational pass
through the particle data at each time step. The code is
based on the Current Advance Method and Cyclic Leapfrog (CAM-CL) code of Matthews (1994).
The code is written in Fortran 77 (+extensions of Fortran 95). There are 1-D, 2-D, and 3-D
versions of the code. The different versions of the code are parallelized
via MPI using spatial and/or particle decompositions; the spatial decomposition
could be in all spatial directions. There is also a hybrid openMP/MPI parallelization.
The code efficiently run on supercomputers like
Marconi (Cineca, Italian supercomputing centre), Jean-Zay (IDRIS, French supercomputing centre).
The output files can be simple
ASCII, binary or HDF5 files, including parallel binary (MPI-IO) and HDF5 outputs.
The boundary conditions could be periodic in all directions; alternatively, in the
x direction there could be reflecting boundary conditions on one side and open boundary
conditions with a continuous injection of particles on the other side (for generation
of shock waves). The simulation box can have also open boundary conditions in
y and z.
Numerical scheme
Fields are defined a grid, the magnetic field B and the ion moments
are on the main grid, (ixΔx, iyΔy, izΔz) (Δx, ...: the spatial resolution) whereas the
electric field E is on the interlaced grid (ixΔx+Δx/2,...).
As electrons are assumed as charge-neutralizing
massless fluids, the electric field is a function
of the magnetic field
the proton charge and current densities ρ and J, respectively,
and of the electron temperature (electrons are usually assumed to be isothermal or
adiabatic). Ions are descibed as (macro)particles using the particle-in-cell scheme.
The (bi/tri-)linear interpolation/weighting is used to determine the interaction
of a particle with the grid and the deposition of the particle contribution to
the moments on the grid.
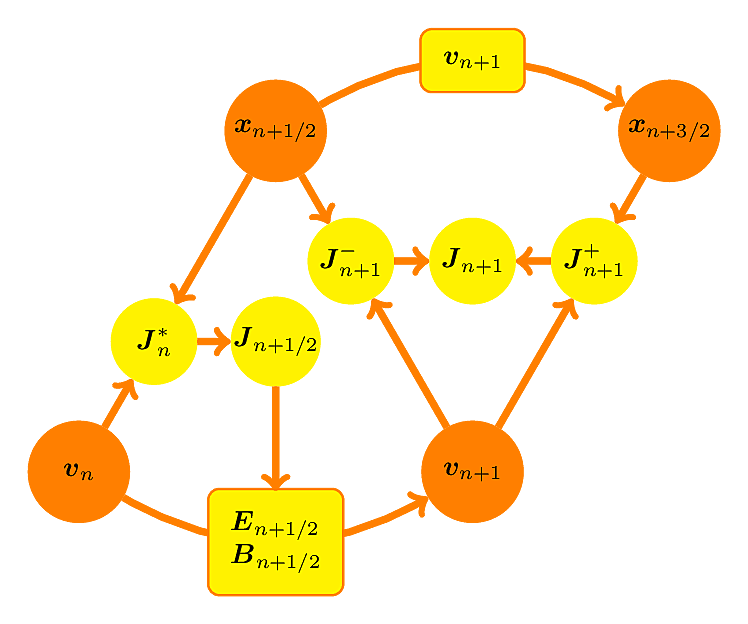
Figure 1:Schematic diagram of the code (Matthews, 1994):
The particle positions and velocities
are taken at the different times
separated by half the time step Δt.
vn,
xn+1/2
At the beginning there are
the current density ρn+1/2= ρ(xn+1/2)
and the "free-streaming" ionic current Jn *
=J (xn+1/2,vn)
as well as
ρn= ρn(xn)
and Jn
=J(xn,vn).
The magnetic field is advanced (using two copies via cyclic leapfrog)
from Bn to Bn+1/2
with E(ρn,Jn,B).
The current advance method advances Jn * to
Jn+1/2.
Using Bn+1/2 and En+1/2=
E(ρn+1/2,Jn+1/2,Bn+1/2)
the particles are advenced using the Boris scheme to
vn+1 and
xn+3/2 and moments are collected.
ρn+3/2=ρ(xn+3/2);
ρn+1is obtained as an average of ρn+1/2
and ρn+3/2. Forward and backward
"free-streaming" ionic currents Jn+1 -
=J (xn+1/2,vn+1) and
Jn+1 +
=J (xn+3/2,vn+1)
are collected and by averaging give Jn+1.
Finally, Bn+1/2 is advanced to Bn+1.
Extensions
The code has two major extensions:
-
Effects of a slow expansion can be modelled
using the expanding box model (Hellinger et al., 2003; Hellinger and Travnicek, 2005).
- Coulomb collisions can be included to the code using the Langevin representation
(Hellinger and Travnicek, 2010, 2015).
Recent results
- Role of ion temperature-anisotropy and beam driven instabilities in the
expanding solar wind (Matteini et al., 2006; Hellinger and Travnicek, 2008, 2011, 2013; Hellinger, 2017),
see Animation 1.

Animation 1: (left) Evolution of the out-of-plane component of the magnetic field in the 2D simulation box.
(middle and right) Evolution
of the system in the plane proton parallel beta and temperature anisotropy (for details see Hellinger, 2017)
- Spectral and heating properties of 2D turbulence from MHD to sub-ion scales (Franci et al., 2015ab)
- Coexistence of plasma turbulence with the oblique fire hose instability
(Hellinger et al., 2015), see Animation 2.
Animation 2: (left and middle) Evolution of the in-plane component of the
fluctuation magnetic and the temperature anisotropy in the 2D simulation box (only a quarter of
the box is shown). The red contours denote the (projected) magnetic field lines. (right) Evolution
of the system in the plane proton parallel beta and temperature anisotropy (for details see Hellinger et al., 2015).
- Correlation between vorticity and proton temperature in 2D kinetic plasma turbulence (Franci et al., 2016a)
- Dependence of the ion-scale spectral break on plasma beta (Franci et al., 2016b).
- Coexistence of plasma turbulence with the mirror instability (Hellinger et al., 2017) see Animation 3.
Animation 3: (left and middle) Evolution of the in-plane and out-of-plane component of the
fluctuation magnetic in the 2D simulation box (only a part of the box is shown). (right) Evolution
of the system in the plane proton parallel beta and temperature anisotropy (for details see Hellinger et al., 2017).
References
- Franci, L., A. Verdini, L. Matteini, S. Landi, and P. Hellinger (2015a), Solar wind turbulence from MHD to sub-ion scales: high-resolution hybrid simulations, Astrophys. J. Lett., 804, L39.
- Franci, L., S. Landi, L. Matteini, A. Verdini, and P. Hellinger (2015b), Hybrid high-resolution simulations of kinetic turbulence at proton scales, Astrophys. J., 812, 21.
- Franci, L., P. Hellinger, L. Matteini, A. Verdini, and S. Landi (2016a), Two-dimensional hybrid simulations of kinetic plasma turbulence: Current and vorticity vs proton temperature, AIP Conference Proceedings, 1720, 040003,
doi:10.1063/1.4943814.
- Franci, L., S. Landi, L. Matteini, A. Verdini, and P. Hellinger (2016b),
Plasma beta dependence of the ion-scale spectral break of solar wind turbulence:
high-resolution 2D hybrid simulations, Astrophys. J., 833, 91.
-
Franci, L., S. Landi, A. Verdini, L. Matteini, and P. Hellinger (2018),
Solar wind turbulent cascade from MHD to sub-ion scales:
large-size 3D hybrid particle-in-cell simulations,
Astrophys. J., 1, 26.
-
Franci, L., P. Hellinger, M. Guarrasi, C. H. K. Chen, E. Papini, A. Verdini,
L. Matteini, and S. Landi (2018), Three-dimensional simulations of solar wind turbulence
with the hybrid code CAMELIA, J. Phys.: Conf. Ser.,
1031, 012002.
-
Hellinger, P., and P. Travnicek (2005),
Magnetosheath compression: Role of characteristic compression time,
alpha particle abundance and alpha/proton relative velocity,
J. Geophys. Res., 110, A04210, doi:10.1029/2004JA010687.
- Hellinger, P., and P. M. Travnicek (2008),
Oblique proton fire hose instability in the expanding solar wind:
Hybrid simulations, J. Geophys. Res., 113, A10109,
doi:10.1029/2008JA013416.
- Hellinger, P., and P. M. Travnicek (2011),
Proton core-beam system in the expanding solar wind:
Hybrid simulations, J. Geophys. Res., 116, A11101, doi:10.1029/2011JA016940.
- Hellinger, P., and P. M. Travnicek (2010), Langevin representation of Coulomb collisions for
bi-Maxwellian plasmas, J. Comput. Phys., 229, 5432–5439.
- Hellinger, P., and P. M. Travnicek (2013),
Protons and alpha particles in the expanding solar wind:
Hybrid simulations, J. Geophys. Res., 118, 5421–5430, doi:10.1002/jgra.50540.
- Hellinger, P., and P. M. Travnicek (2015), Proton temperature-anisotropy-driven instabilities in weakly collisional plasmas: Hybrid simulations, J. Plasma Phys., 81, 305810103.
- Hellinger, P., P. Travnicek, A. Mangeney, and R. Grappin (2003), Hybrid simulations of the expanding solar wind:
Temperatures and drift velocities, Geophys. Res. Lett., 30, 1211, doi:10.1029/2002GL016409.
- Hellinger, P., L. Matteini, S. Landi, A. Verdini, L. Franci, and P. M. Travnicek (2015), Plasma turbulence and kinetic instabilities at ion scales in the expanding solar wind, Astrophys. J. Lett., 811, L32.
- Hellinger, P., S. Landi, L. Matteini, A. Verdini, and L. Franci (2017), Mirror instability in the turbulent solar wind,
Astrophys. J., 838, 158.
- Hellinger, P. (2017), Proton fire hose instabilities in the expanding solar wind, J. Plasma Phys., 83, 705830105.
- Matteini, L., S. Landi, P. Hellinger, and M. Velli (2006), Parallel proton fire hose instability in the expanding solar wind: Hybrid simulations, J. Geophys. Res., 111, A10101, doi:10.1029/2006JA011667.
- Matthews, A. (1994), Current advance method and cyclic leapfrog for 2D
multispecies hybrid plasma simulations, J. Comput. Phys.,
112, 102–116.
See also here for more publications.



